填空题1. 四元齐次线性方程组
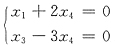
的基础解系______.
(0,1,0,0)T,(-2,0,3,1)T
[解析] 由齐次方程组的系数矩阵
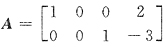
易见秩r(A)=2,那么n-r(A)=4-2=2,故基础解系由两个线性无关的解向量所构成,且每个解中有两个自由变量.由于1、3两列所构成的二阶子式
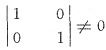
故可取x
2,x
4为自由变量.
令x
2=1,x
4=0,由第二个方程x
3-3x
4=0求出x
3=0.再把x
2=1,x
4=0,x
3=0代人第一个方程x
1+2x
4=0求出x
4=0,于是得到解η
1=(0,1,0,0)
T,
令x
2=0,x
4=1由第二个方程x
3-3x
4=0求出x
3=3,再将x
2=0,x
4=1,x
3=3代人第一个方程x
1+2x
4=0,求出x
1=-2,于是得到解η
2=(-2,0,3,1)
T.
所以Ax=0的基础解系是η
1,η
2.
2. 已知齐次线性方程组
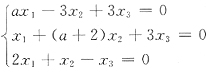
有无穷多解,则a=______.
-5或-6
[解析] 齐次方程组Ax=0有无穷多解的充分必要条件是r(A)<n.现在是三个未知数三个方程的齐次方程组,故可以用系数行列式|A|=0.
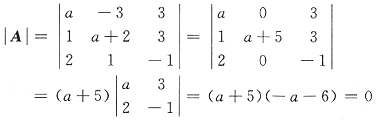
故a=-5或a=-6.
3. 已知方程组
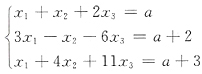
有无穷多解,那么a=______.
3
[解析] 线性方程组Ax=b有无穷多解的充要条件是
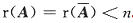
.对增广矩阵作初等行变换,有
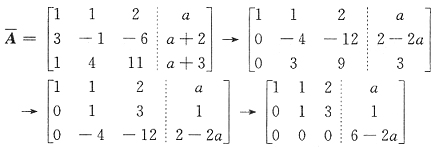
由于r(A)=2,而
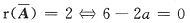
所以,方程组有无穷多解的充分必要条件是a=3.
4. 已知方程组
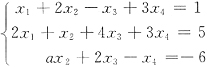
无解,则a=______.
-1
[解析] 非齐次线性方程组Ax=b无解的充分必要条件是
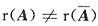
.对增广矩阵作初等行变换有
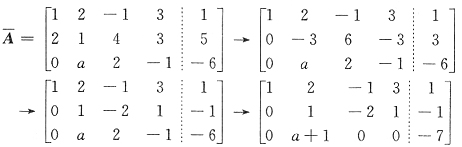
可见a=-1时,r(A)=2,
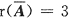
,线性方程组无解,所以应当填a=-1.
5. 设α
1=(6,-1,1)
T与α
2=(-7,4,2)
T是线性方程组
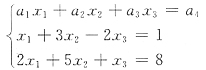
的两个解,那么此方程组的通解是______.
(6,-1,1)T+k(13,-5,-1)T(k为任意常数)
(或(-7,4,2)T+k(13,-5,-1)T,k为任意常数)
[解析] 一方面因为α
1,α
2是非齐次线性方程组Ax=b的两个不同的解,故必有
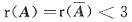
.另一方面由于在系数矩阵A中存在二阶子式
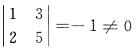
又必有r(A)≥2,因此,必有
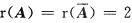
.
那么,n-r(A)=3-2=1,因此,导出组Ax=0的基础解系由一个解向量所构成,根据解的性质
α
1-α
2=(6,-1,1)
T-(-7,4,2)
T=(13,-5,-1)
T 是导出组Ax=0的非零解,即基础解系,那么再根据解的结构,知
(6,-1,1)
T+k(13,-5,-1)
T(k为任意常数)
是方程组的通解.(或(-7,4,2)
T+k(13,-5,-1)
T)
6. 设A
n×nx=0,其中|A|=0,余子式M
1n≠0,则Ax=0的通解是______.
k[M11,-M12,…,(-1)n+1M1n]T,其中k是任意常数
[解析] |A|=0,AA*=|A|E=0,A*的任一列都是Ax=0的解.
因|A|=0,M1n≠0,故r(A)=n-1.故通解为k(A11,A12,…,A1n)T=k(M11,-M12,…,(-1)n+1M1n)T,k是任意常数.
7. 设线性方程组A
3×4x=b,即
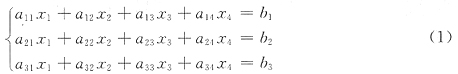
有通解k[1,2,-1,1]
T+[1,-1,0,2]
T,其中k是任意常数,则方程组B
3×3x=b即
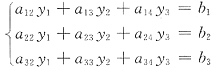
有一个特解是______.
(-3,1,1)T
[解析] 由观察,方程组(2)比方程组(1)减少了一个未知量.若方程组(2)有解ζ=(a,b,c)T,则η=(0,a,b,c)T必是方程组(1)的解,现已知方程组(1)有无穷多解k(1,2,-1,1)T+(1,-1,0,2)T,其中k是任意常数,选择任意常数k,使(1)的解的第一个分量为0,即选k=-1,得(1)的一个特解为(0,-3,1,1)T,则向量(-3,1,1)T满足方程组(2),是方程组(2)的一个特解.故向量(-3,1,1)T即为所求.
8. 设线性方程组A
3×3=b,即
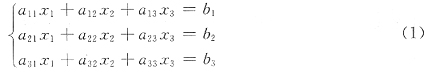
有唯一解ξ=[1,2,3]
T.
方程组B
3×4y=b即
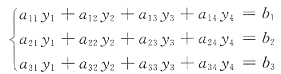
有特解η=[-2,1,4,2]
T,则方程组(2)的通解是______.
k(-3,-1,1,2)T+(-2,1,4,2)T,其中k是任意常数
[解析] 方程组(1)Ax=b有唯一解ξ=[1,2,3]T,故r(A)=r(A|b)=3.By=b有特解η=[-2,1,4,2],显然r(B)=r(B|b)=3,且η1=(1,2,3,0)T是方程组B3×4y=b的另一个特解.
B是3×4矩阵,故对应齐次方程组Bx=0的基础解系只有一个线性无关向量组成,且是η-η1故(2)的通解为
k(η-η1)+η=k(-3,-1,1,2)T+(-2,1,4,2)T
9. 设r(A
3×3)=2,方程组Ax=b有解η
1,η
2,η
3,其中η
1+η
2=(4,2,3)
T,η
2+η
3=(5,7,-3)
T,则Ax=b的通解是______.
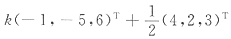
,其中k是任意常数
[解析] A
3×3x=b,r(A)=2,方程组通解的形式为kξ+η.则ξ=(η
1+η
2)-(η
2+η
3)=(-1,-5,6)
T是对应齐次方程组Ax=0的基础解系
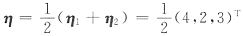
,是Ax=b的一个特解.
故通解为

,其中k是任意常数.
10. 设A=[a
ij]是三阶正交矩阵,其中a
33=-1,b=(0,0,5)
T,则线性方程组Ax=b的解是______.
(0,0,-5)T
[解析] 法一 由正交矩阵定义:AA
T=A
TA=E,知A的列向量与行向量都是单位向量,故
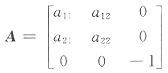
故方程组Ax=b有解
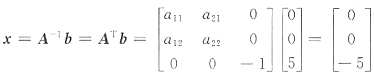
法二 由法一
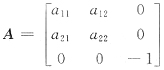
,
由克拉默法则
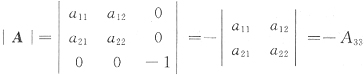
,
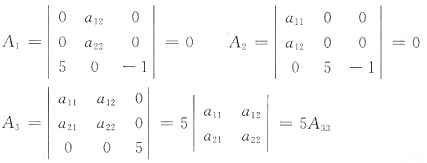
得解

故x=(0,0,-5)
T.
11. 已知齐次线性方程组
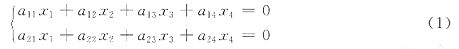
有通解,k
1(2,-1,0,1)
T+k
2(3,2,1,0)
T,则方程组
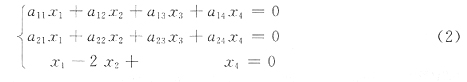
的通解是______.
k(17,9,5,1)T,k是任意常数
[解析] 方程组(2)的通解必在方程组(1)的通解之中,是方程组(1)的通解中满足(2)
中第3个方程的解,令(1)的通解

满足(2)的第3个方程,得
(2k
1+3k
2)-2(-k
1+2k
2)+0k
2+k
1=0
得5k
1=k
2 代入(1)的通解,得方程组(2)的通解为
k
1(2,-1,0,1)
T+5k
1(3,2,1,0)
T=k
1(17,9,5,1)
T (其中k
1是任意常数).
12. 已知方程组
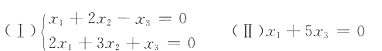
那么(Ⅰ)与(Ⅱ)的公共解是______.
k(-5,3,1)T,k为任意常数
[解析] 所谓方程组(Ⅰ)与(Ⅱ)的公共解,即这两个方程组解集合的交集,把(Ⅰ)与(Ⅱ)联立得到方程组(Ⅲ),那么方程组(Ⅲ)的解就是(Ⅰ)与(Ⅱ)的公共解.对方程组(Ⅲ)的系数矩阵作初等行变换,有

由于秩r(A)=2,n-r(A)=1,取x
3为自由变量,令x
3=1,代入求解得x
2=3,x
1=-5,所以,方程组(Ⅲ)的基础解系是
η=(-5,3,1)
T 那么(Ⅰ)与(Ⅱ)的公共解是:kη,k为任意常数.
13. 已知非齐次线性方程组(Ⅰ)与(Ⅱ)同解,其中
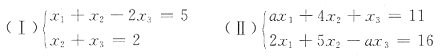
则a=______.
1
[解析] 所谓两个方程组(Ⅰ)与(Ⅱ)同解,即(Ⅰ)的解全是(Ⅱ)的解,(Ⅱ)的解也全是(Ⅰ)的解.对(Ⅰ)求出其通解
(3,2,0)
T+k(3,-1,1)
T=(3k+3,2-k,k)
T.
把x
1=3+3k,x
2=2-k,x
3=k代入方程组(Ⅱ),有
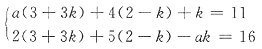
整理为
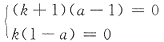
因为k为任意常数,故a=1.此时方程组(Ⅰ)的解全是方程组(Ⅱ)的解.
且当a=1时,方程组(Ⅱ)为
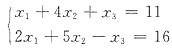
由r(A
2)=2,从解的结构知(Ⅱ)的通解形式为α+kη和(Ⅰ)的通解结构相同.(Ⅰ)的通解已满足(Ⅱ),也是(Ⅱ)的通解,故(Ⅰ),(Ⅱ)有同解.
或者易于验算α=(3,2,0)
T是A
2x=b的解,η=(3,-1,1)
T是A
2x=0.
所以(Ⅰ)与(Ⅱ)同解.
14. 已知

,A*是A的伴随矩阵,那么A*的特征值是______.
1,7,7
[解析] (解法一) 按伴随矩阵定义,由代数余子式
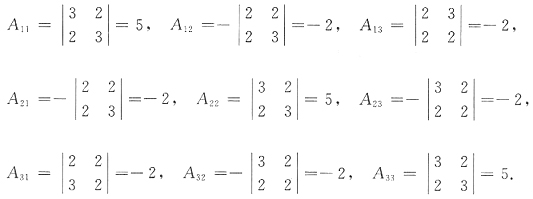
知伴随矩阵
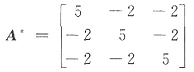
那么

所以A
*的特征值是1,7,7.
(解法二)由矩阵A的特征多项式
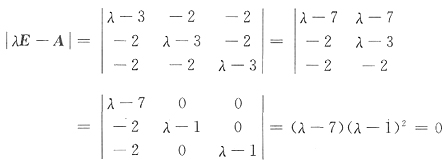
由|A|=Πλ
i,从而|A|=7·1·1=7.
因为若Aα=λα,则有
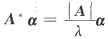
.所以A
*的特征值是1,7,7.
(解法三)因为
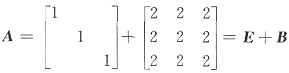
由秩r(B)=1,知B的特征值是6,0,0.故A的特征值是7,1,1.
下同解法二.
15. 已知三阶矩阵A的特征值是
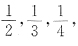
又三阶矩阵B满足关系式A
-1BA=6A+BA.则矩阵B的特征值是______.
6,3,2
[解析] 由
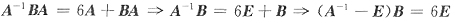
知B=6(A
-1-E)
-1 因为A的特征值
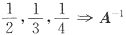
的特征值
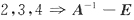
的特征值1,2,3

(A
-1-E)
-1的特征值
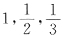
,
所以矩阵B的特征值:6,3,2.
16. 设A是主对角线元素之和为-5的三阶矩阵,且满足A
2+2A-3E=0,那么矩阵A的三个特征值是______.
1,-3,-3
[解析] 设λ是矩阵A的特征值,α是相对应的特征向量,即Aα=λα,α≠0.
那么根据Anα=λnα,由A2+2A-3E=0有(λ2+2λ-3)α=0,又因α≠0.
故λ2+2λ-3=(λ+3)(λ-1)=0.
知λ取值范围为1和-3,再由∑λi=∑aii=-5,知矩阵A的特征值是1,-3,-3.
17. 已知α=(a,1,1)
T是矩阵
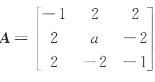
的逆矩阵的特征向量,那么α在矩阵A中对应的特征值是______.
-5
[解析] 设α是矩阵A
-1属于特征值λ
0的特征向量,按定义有A
-1α=λ
0α,于是α=λ
0Aα.即
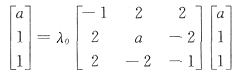
即
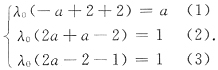
由(2)知λ
0≠0,(2)-(3)易见a=-1,那么

.因为A和A
-1特征值互为倒数,故α是矩阵A中λ=-5所对应的特征向量.
18. 设α=(1,-1,a)
T是
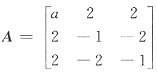
的伴随矩阵A*的特征向量,其中r(A*)=3,则a=______.
-1
[解析] α是A
*的特征向量,设对应的特征值为λ
0,则有A
*α=λ
0α.两边左乘A,得AA
*α=λ
0Aα=|A|α.即
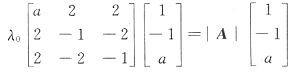
得
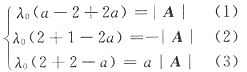
因r(A
*)=3,|A
*|≠0,故λ
0≠0,由(1)(2)式解得a=-1,(λ
0=-5)
19. 设A是3阶矩阵,α
1,α
2,α
3是3维线性无关的列向量,且
Aα
1=α
1,Aα
2=-α
3,Aα
3=α
2+2α
3 则矩阵A的三个特征值是______.
1,1,1
[解析] 由已知条件,有
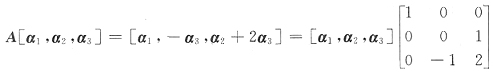
因为α
1,α
2,α
3线性无关,故矩阵P=[α
1,α
2,α
3]可逆.记
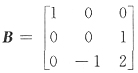
,
那么由AP=PB得P
-1AP=B,即A~B.
因为
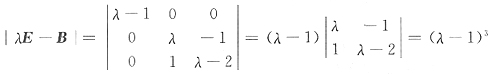
矩阵B的特征值1,1,1,因相似矩阵有相同的特征值,所以矩阵A的特征值为1,1,1.
20. 已知α是3维列向量,αT是α的转置,若矩阵αα
T相似于
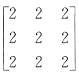
,则α
Tα=______.
6
[解析] 设α=(a
1,a
2,a
3)
T,记A=αα
T,有
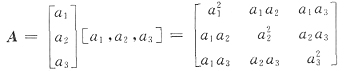
又
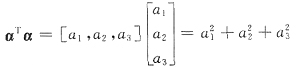
可见α
Tα是矩阵A主对角线元素之和,即矩阵A的迹tr(A)由于相似矩阵迹相同,所以本题中α
Tα=2+2+2=6.
21. 已知A是三阶方阵,其特征值分别为1,2,-3,则行列式|A|中主对角线元素的代数余子式之和A
11+A
22+A
33=______.
-7
[解析] 由伴随矩阵定义
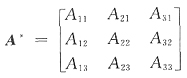
又∑a
ii=∑λ
i,故只需求出伴随矩阵A
*的特征值之和也就是代数余子式A
11+A
22+A
33之和.
由|A|=Πλ
i=1·2·(-3)故A
*的特征值
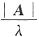
:-6,-3,2,故A
11+A
22+A
33=(-6)+(-3)+2=-7.
22. 设
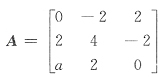
有二重特征值,则a=______.
[解析]
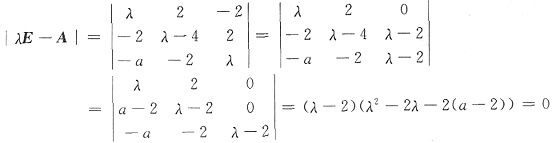
若λ=2是二重根,则有λ
2-2λ-2(a-2)|
λ=2=0,得a=2
若λ
2-2λ-2(a-2)=0是完全平方,则有(λ-1)
2=0,(即λ=1是二重根)则有-2(a-2)=1,得
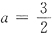
.
23. 设A是三阶实对称矩阵,存在正交阵Q=[ξ
1,ξ
2,ξ
3],使得Q
-1AQ=Q
TAQ=

,则矩阵
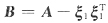
的特征值是______.
0,2,3
[解析] 由题设条件知,有特征值λ
1=1,λ
2=2,λ
3=3,对应的特征向量分别是ξ
1,ξ
2,ξ
3,即有
Aξ
i=λ
iξ
i=iξ
i,i=1,2,3
又Q是正交矩阵,ξ
1,ξ
2,ξ
3满足条件
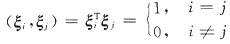
故

故
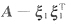
有特征值0,2,3.
24. 设α=(1,-1,a)
T,β=(1,a,2)
T,A=E+αβ
T,且λ=3是矩阵A的特征值,则矩阵A属于特征值λ=3的特征向量是______.
k(1,1,1)T,k≠0
[解析] 令B=αβT,由于秩r(B)=1,且βTα=a+1知矩阵B的特征值为a+1,0,0.那么A=E+B的特征值为a+2,1,1.
因为λ=3是矩阵A的特征值,故a+2=3,知a=1.
那么βα=(αβT)α=α(βTα)=2α
α=(1,-1,1)T是矩阵B属于特征值λ=2的特征向量,也就是矩阵A属于特征值λ=3的特征向量.
25. 已知矩阵A=
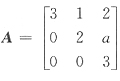
和对角矩阵相似,则a=______.
-2
[解析] 因为
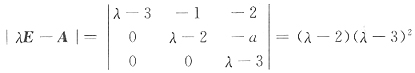
所以矩阵A的特征值为2,3,3.因为矩阵A的特征值有重根,所以

那么

可见a=-2.
26. 已知A是四阶实对称矩阵,秩r(A)=3,矩阵A满足A
4-A
3-A
2-2A=0则与A相似的对角矩阵是______.
[解析] 设Aα=λα,α≠0,那么由A
nα=λ
nα有
(λ
4-λ
3-λ
2-2λ)α=0,α=0
从而λ
4-λ
3-λ
2-2λ)=0.即λ(λ-2)(λ
2+λ+1)=0
再由秩r(A)=3,可知特征值必为2,2,2,0.A是实对称矩阵,故
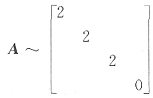
.
27. 已知矩阵
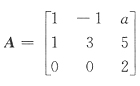
只有一个线性无关的特征向量,那么A的三个特征值是______.
2,2,2
[解析] 根据定理“若A有n个不同的特征值,则A有n个线性无关的特征向量”,现因为矩阵A只有一个线性无关的特征向量,所以A的特征值必是三重根,否则A至少有两个不同的特征值,那么至少有两个线性无关的特征向量.
由于∑aii=∑λi,故1+3+2=λ+λ+λ,即知λ1=λ2=λ3=2.
28. 已知
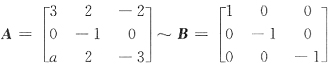
,则a=______.
4
[解析] 由题设条件知,A有特征值λ
1=1,λ
2=λ
3=-1,将λ
1=1代人特征方程,得
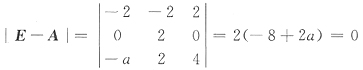
得a=4.
29. A是三阶矩阵,ξ,α,β是三个三维线性无关的列向量,其中Ax=0有解ξ,Ax=β有解α,Ax=α有解β,则A~______.
[解析] ξ,α,β线性无关,都是非零向量,Ax=0有解ξ,即Aξ=0=0ξ,故A有λ
1=0,(对应的特征向量为ξ),又Ax=β有解α,即Aα=β,Ax=α有解β,即Aβ=α,且A(-β)=-α.从而有
A(α+β)=β+α=(α+β)
(A(α-β)=β-α=-(α-β)
故知A有λ
2=1,λ
3=-1,(α+β,α-β均是非零向量,是对应的特征向量),三阶矩阵A有三个不同的特征值,0,1,-1.故
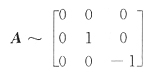
30. 已知
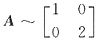
,则B=(A-E)(A-2E)=______.
0
[解析] 因A~Λ,故知存在可逆阵P,使P-1AP=Λ,A=PΛP-1代入B,得
B=(A-E)(A-2E)=(PΛP-1-E)(PΛP-1-2E)
31. 设
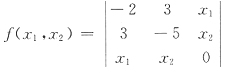
,则二次型的对应矩阵是______.
[解析] 展开行列式,写出二次型的一般表述式,再写出对应矩阵.
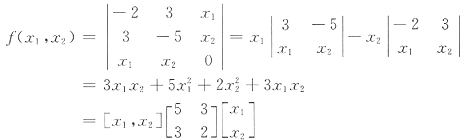
,故f的对应矩阵为
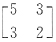
.
32. 已知三元二次型
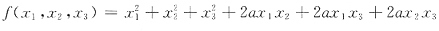
的秩为2,则二次型的正惯性指数p=______.
2
[解析] 二次型矩阵
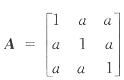
由于二次型的秩为2,即矩阵A的秩为2.那么
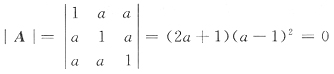
显然a=1时r(A)=1,不合题意,故

当
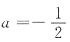
时
因为
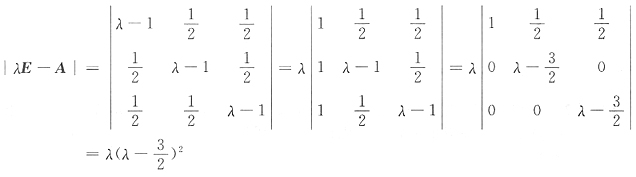
所以矩阵A的特征值为
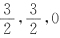
,故p=2.
33. 二次型
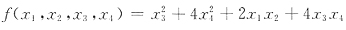
的规范形是______.
[解析] 二次型矩阵
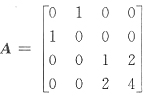
由于|λE-A|=(λ
2-1)(λ
2-5λ)
知矩阵A的特征值为:1,5,-1,0.故二次型正惯性指数p=2,负惯性指数q=1.
因此二次型的规范形为
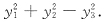
或利用配方法.
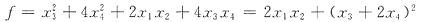
令
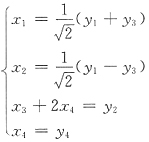
得f的规范形为
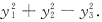
34. 已知二次型
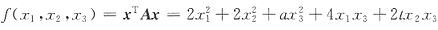
经正交变换x=Py可化成标准形
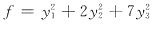
,则t=______.
±1
[解析] 因为二次型x
TAx经正交变换化为标准形时,标准形中平方项的系数就是二次型矩阵A的特征值,所以1,2,7是A的特征值.
又因经过正交变换二次型的矩阵不仅合同而且还相似,因此有

根据相似矩阵的性质,有
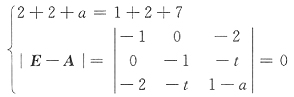
即:a=6,t
2=1,所以应填±1.
35. 若二次型
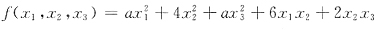
是正定的,则a的取值范围是______.
[解析] 二次型f的矩阵为
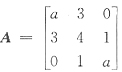
因为f正定
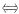
A的顺序主子式全大于零,即
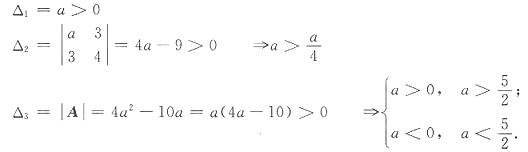
故
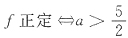
36. 设α=(1,0,1)
T,A=αα
T、,若B=(kE+A)*是正定矩阵,则k的取值范围是______.
k<-2或k>0
[解析] 由于
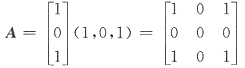
有|λE-A|=λ
3-2λ
2=λ
2(λ-2)
即矩阵A的特征值是2,0,0,从而矩阵kE+A的特征值是k+2,k,k,那么B=(kE+A)
*的特征值是k
2,k(k+2),k(k+2).
所以,B正定的充要条件是:k
2>0,k(k+2)>0.得k<-2或k>0.
37. 已知矩阵
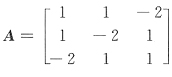
与二次型
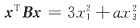
的矩阵B合同,则a的取值______.
a<0
[解析] 矩阵A与B合同
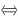
x
TAx与x
TBx有相同的正、负惯性指数.
由于
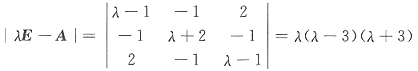
可见p
A=1,q
A=1.因而
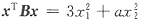
的p
B=1,q
B=1时,矩阵A和B合同.
所以a<0即可.
38. 已知
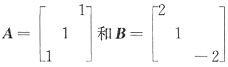
合同,那么使C
TAC=B的可逆矩阵C=______.
[解析] 二次型x
TAx经坐标变换(或称可逆线性变换),x=Cy得x
TAx=y
TBy就有A和B合同,其中B=C
TAC,那么求矩阵C就是求所用坐标变换(由于本题矩阵A和B不相似,若先用正交变换过渡是可行的,但比较麻烦).
对二次型
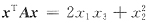
用配方法,令
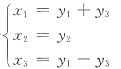
即有
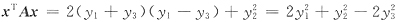
可见经坐标变换

,就有矩阵A和B合同,所以
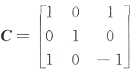
39. 设A是三阶实对称矩阵,满足A
3=2A
2+5A-6E,保证kE+A是正定阵,则k的取值范围是______.
k>2
[解析] 由题设条件A3=2A2+5A-6E,即
A3-2A2-5A+6E=0
设A有特征值λ,则λ满足
λ3-2λ2-5λ+6=0
因式分解得λ3-2λ2-5λ+6=(λ-1)(λ+2)(λ-3)=0
故A的特征值的取值范围是1,-2,3.kE+A的特征值的取值范围是k+1,k-2,k+3,当k>2时,kE+A的特征值均大于零,故k>2.
40. 设A是m×n矩阵,E是n阶单位阵,矩阵B=-aE+A
TA是正定阵,则a的取值范围是______.
a<0
[解析] B
T=(-aE+A
TA)
T=-aE+A
TA=B.B是对称阵.
B正定

对任给的x≠0,有
x
TBx=x
T(-aE+A
TA)x=-ax
Tx+x
TA
TAx=-ax
Tx+(Ax)
TAx>0 (*)
其中(Ax)
T(Ax)≥0,x
Tx>0,
故(*)式成立,a的取值范围应-a>0,即a<0.
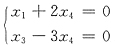 的基础解系______.
的基础解系______.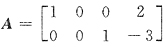
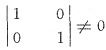
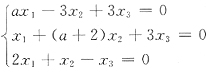 有无穷多解,则a=______.
有无穷多解,则a=______.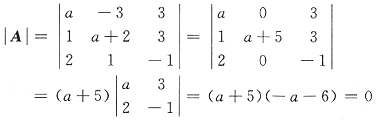
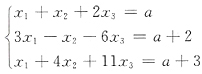 有无穷多解,那么a=______.
有无穷多解,那么a=______.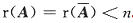 .对增广矩阵作初等行变换,有
.对增广矩阵作初等行变换,有
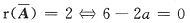
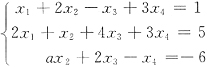 无解,则a=______.
无解,则a=______.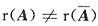 .对增广矩阵作初等行变换有
.对增广矩阵作初等行变换有
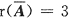 ,线性方程组无解,所以应当填a=-1.
,线性方程组无解,所以应当填a=-1.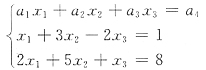
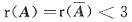 .另一方面由于在系数矩阵A中存在二阶子式
.另一方面由于在系数矩阵A中存在二阶子式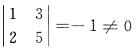
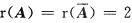 .
.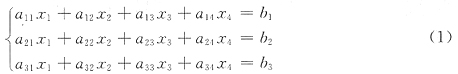
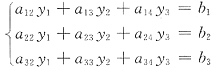
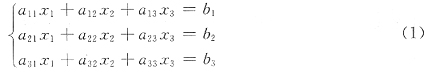
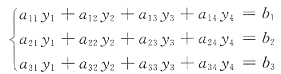
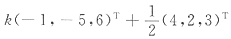 ,其中k是任意常数
,其中k是任意常数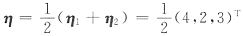 ,是Ax=b的一个特解.
,是Ax=b的一个特解. ,其中k是任意常数.
,其中k是任意常数.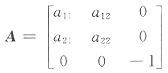
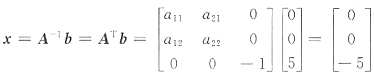
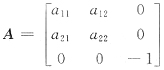 ,
,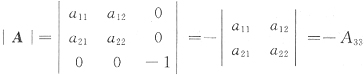 ,
,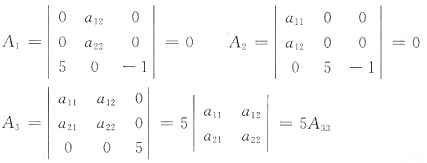

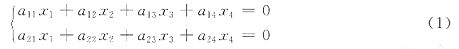
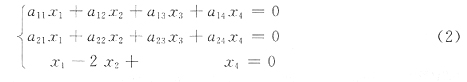

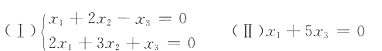

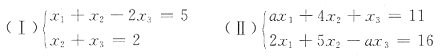
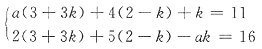
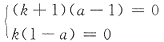
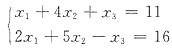
 ,A*是A的伴随矩阵,那么A*的特征值是______.
,A*是A的伴随矩阵,那么A*的特征值是______.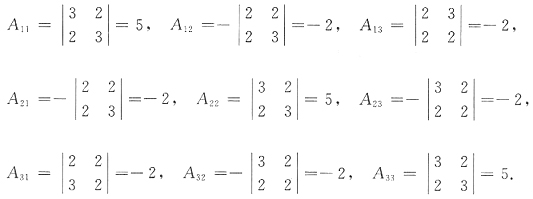
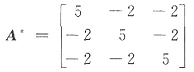

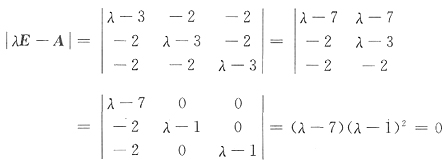
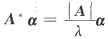 .所以A*的特征值是1,7,7.
.所以A*的特征值是1,7,7.
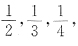 又三阶矩阵B满足关系式A-1BA=6A+BA.则矩阵B的特征值是______.
又三阶矩阵B满足关系式A-1BA=6A+BA.则矩阵B的特征值是______.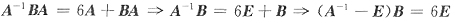
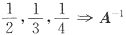 的特征值
的特征值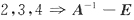 的特征值1,2,3
的特征值1,2,3 (A-1-E)-1的特征值
(A-1-E)-1的特征值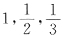 ,
,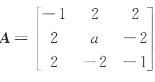 的逆矩阵的特征向量,那么α在矩阵A中对应的特征值是______.
的逆矩阵的特征向量,那么α在矩阵A中对应的特征值是______.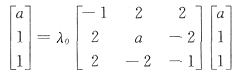
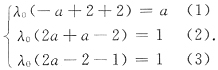
 .因为A和A-1特征值互为倒数,故α是矩阵A中λ=-5所对应的特征向量.
.因为A和A-1特征值互为倒数,故α是矩阵A中λ=-5所对应的特征向量.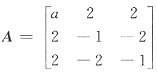 的伴随矩阵A*的特征向量,其中r(A*)=3,则a=______.
的伴随矩阵A*的特征向量,其中r(A*)=3,则a=______.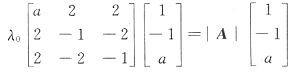
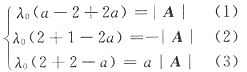
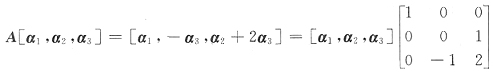
 ,
,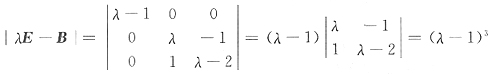
 ,则αTα=______.
,则αTα=______.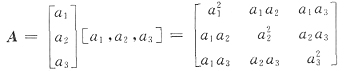
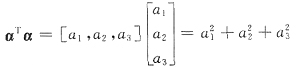
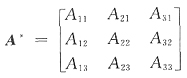
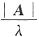 :-6,-3,2,故A11+A22+A33=(-6)+(-3)+2=-7.
:-6,-3,2,故A11+A22+A33=(-6)+(-3)+2=-7. 有二重特征值,则a=______.
有二重特征值,则a=______.
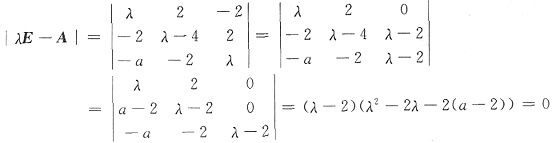
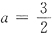 .
. ,则矩阵
,则矩阵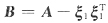 的特征值是______.
的特征值是______.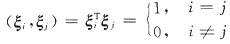

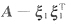 有特征值0,2,3.
有特征值0,2,3.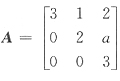 和对角矩阵相似,则a=______.
和对角矩阵相似,则a=______.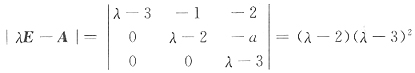

 可见a=-2.
可见a=-2.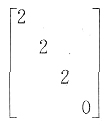
 .
.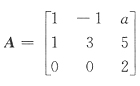 只有一个线性无关的特征向量,那么A的三个特征值是______.
只有一个线性无关的特征向量,那么A的三个特征值是______.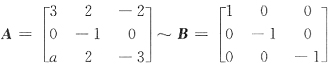 ,则a=______.
,则a=______.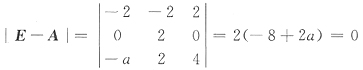
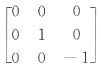
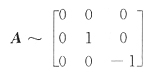
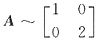 ,则B=(A-E)(A-2E)=______.
,则B=(A-E)(A-2E)=______.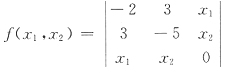 ,则二次型的对应矩阵是______.
,则二次型的对应矩阵是______.
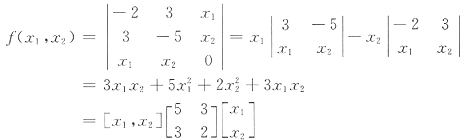 ,故f的对应矩阵为
,故f的对应矩阵为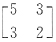 .
.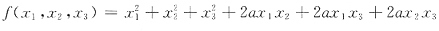 的秩为2,则二次型的正惯性指数p=______.
的秩为2,则二次型的正惯性指数p=______.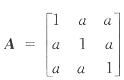 由于二次型的秩为2,即矩阵A的秩为2.那么
由于二次型的秩为2,即矩阵A的秩为2.那么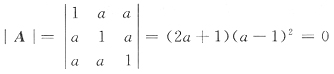

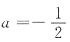 时
时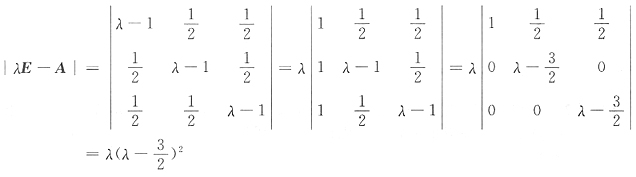
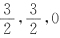 ,故p=2.
,故p=2.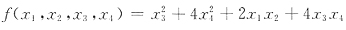 的规范形是______.
的规范形是______.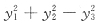
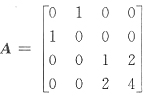
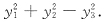
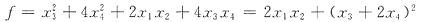
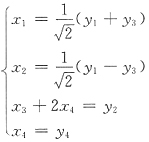
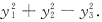
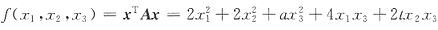 经正交变换x=Py可化成标准形
经正交变换x=Py可化成标准形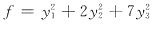 ,则t=______.
,则t=______.
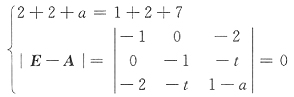
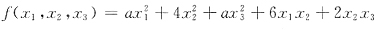 是正定的,则a的取值范围是______.
是正定的,则a的取值范围是______.
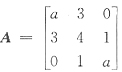
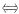 A的顺序主子式全大于零,即
A的顺序主子式全大于零,即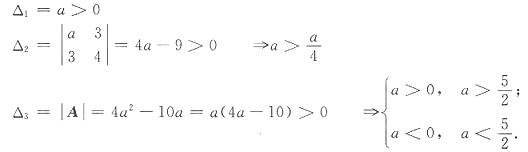
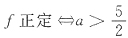
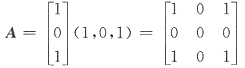
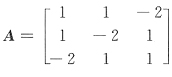 与二次型
与二次型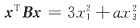 的矩阵B合同,则a的取值______.
的矩阵B合同,则a的取值______.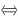 xTAx与xTBx有相同的正、负惯性指数.
xTAx与xTBx有相同的正、负惯性指数.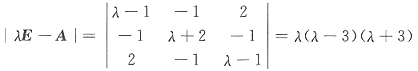
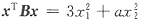 的pB=1,qB=1时,矩阵A和B合同.
的pB=1,qB=1时,矩阵A和B合同.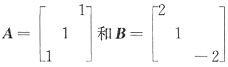 合同,那么使CTAC=B的可逆矩阵C=______.
合同,那么使CTAC=B的可逆矩阵C=______.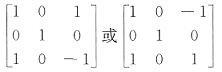
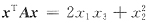
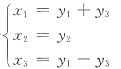
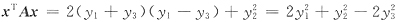
 ,就有矩阵A和B合同,所以
,就有矩阵A和B合同,所以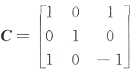
 对任给的x≠0,有
对任给的x≠0,有