一、单项选择题(在每小题列出的四个备选项中只有一个是最符合题目要求的)1. 下列等式成立的是______
A.(e
x)
2=e
x2 B.(e
x)
2=e
2x C.
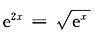
D.
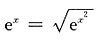
A B C D
B
[考点] 指数函数的基本运算法则
[解析] (ex)2=e2x,故选B.
3. 极限
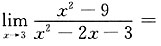
______
A.0
B.
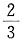
C.
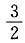
D.

A B C D
C
[考点] 函数的极限
[解析]
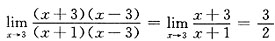
.
6. 某产品产量为q时总成本
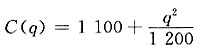
,则q=1200时的边际成本为______
A.0
B.
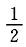
C.1
D.2
A B C D
D
[考点] 边际成本的概念
[解析] 边际成本
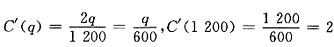
.
8. 极限
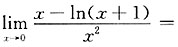
______
A.
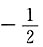
B.0
C.
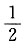
D.1
A B C D
C
[考点]

型,洛必达法则
[解析]
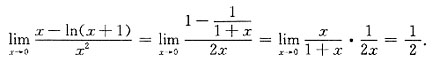
10. 设函数z=ln(x
2+y
2),则
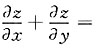
______
A.
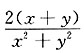
B.

C.
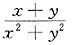
D.
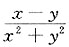
A B C D
A
[考点] 偏导数
[解析]
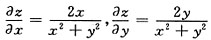
则
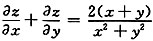
.
三、计算题1. 求a的值,使得函数
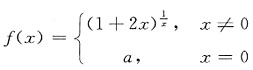
在x=0处连续.
解:
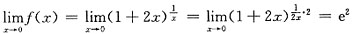
,
由于函数f(x)在x=0处连续,且f(0)=a,故a=e
2.
2. 已知函数y=f(sinx),且f具有二阶导数,求y".
解:y=f(sinx),
y'=f'(sinx)·cosx,
y"=f"(sinx)·cos2+f'(sinx)(-sinx)
=f"(sinx)·cos2x-f'(sinx)·sinx.
3. 求函数f(x)=ln(x
2+1)在区间[-1,2]上的最大值和最小值.
解:f(x)=ln(x
2+1),
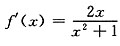
,令f'(x)=0,得x=0,f(0)=ln1=0,
x=0把区间[-1,2]分成2个区间,列表如下:

此题极小值点为最小值点,故函数f(x)在区间[-1,2]上的最小值为0,最大值为ln5.
4. 求曲线
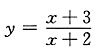
的水平和铅直渐近线.
解:水平渐近线
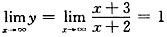
,故直线y=1为曲线
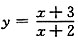
的水平渐近线.
由于
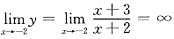
,故直线x=-2为曲线
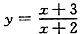
的铅直渐近线.
5. 设z=z(x,y)是由方程x
2-3xyz-1=0所确定的隐函数,求偏导数
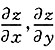
.
解:z
3-3xyz-1=0

:方程两端关于变量x求导,y看作常数,z看作中间变量.
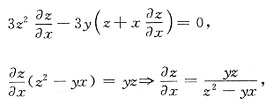
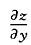
:同理,
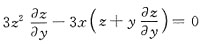
,
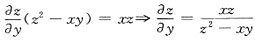
.